(2)设甲、乙两地的图上距离应该是x厘米。
x:5000000=1:1000000
1000000x=5000000
x=5
或5000000×1000000/1=5(厘米)
答:(1)这幅地图的比例尺是1:500000;(2)甲、乙两地的图上距离应该是5厘米。
3.正、反比例应用题
(1)正比例应用题
含有成正比例关系的量,并根据正比例的意义、性质列出比例来解答的应用题,叫做成正比例关系的应用题。
成正比例关系的应用题,可以根据成正比例的意义“两种量中相对应的两个数的比值一定”,列出比例解答。
(2)反比例应用题
含有成反比例关系的量,并根据反比例的意义、性质列出比例来解答的应用题,叫做成反比例关系的应用题。
成反比例关系的应用题,可以根据成反比例的意义“两种量中相对应的两个数的乘积一定”列出比例解答。
(3)正、反比例应用题的特征及解题关键
正、反比例应用题的特征是:在一道正(或反)比例应用题中,有一种(或隐含一种)不变的量,即常数k。
解题关健:先根据题意正确判断是否是正、反比例应用题,判断题中相对应的量成什么比例关系,再根据“比值一定”或“乘积一定”列出相应比例解答。
(4)正、反比例应用题的解题步骤
①分析题意,找出题中的定量和两种相关联的量;
②判断题目中两种相关联的量是成正比例还是成反比例;
③设未知量为x,并注明单位;
④根据正、反比例的意义列出比例,并解比例;
⑤检验,写出答案。
例3下表是将一根木料锯成的段数与锯的次数之间的关系分析表。
(1)请你根据实际生活经验完成此表。
(2)若将一根木料锯成5段要8分钟,那么锯成6段需要多少分钟?

分析 这是一道比例应用题,考查用比例知识灵活解答实际问题的能力。锯成的段数与用的时间不直接成比例。解答这道题需要在生活中善于观察、发现规律,并具有一定的创新意识。锯成的段数与所用次数的数量关系是:锯的次数=锯的段数一1。锯的次数与需用的时间成正比例关系。
解:(1)填表如下:

(2)设锯成6段需要x分钟,则:
5-1/8=6-1/x
x=10
答:锯成6段需要10分钟。
例4 客车和货车分别从甲、乙两地同时相对开出,经过若干小时在途中相遇,相遇后又行5小时货车到达甲地,这时客车到乙地后又掉头行了甲、乙两地距离的25%。客车和货车从出发到相遇用了多少小时?
分析与解 此题综合性较强,要求学生能抓住两车行驶中的实质问题。题中两车行的时间始终保持一致,所以客车与货车所行的路程比为(1+25%):1=5:4,就是两车的速度比。相遇后货车所行的路程和相遇时客车所行路相同,在这段路上两车所用时间和它们的速度成反比,行这段路程客车与货车所用时间比是4:5,客车在此段上所用时间就是相遇时间。如下图:
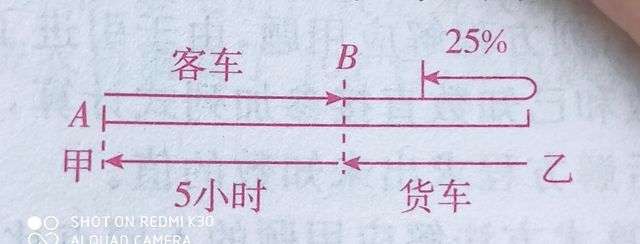
客车、货车速度比:(1+25%):1=5:4
行AB这段路,客车和货车所需时间比:4:5相遇时间:5÷5×4=4(时)
答:客车和货车从出发到相遇用了4小时。