Blies.,Www ...后期图画风了,so不怎么标准w😭
相关知识链接
1.杠杆的五要素:支点、动力、阻力、动力臂、阻力臂。
2.力臂的作法:一找点,二画线,三作垂线段。
3.杠杆的平衡条件:F1l1=F2l2。
4.省力杠杆:省力费距离;费力杠杆:费力省距离;等臂杠杆:不省力也不省距离。
方法技巧
识别定滑轮和动滑轮的依据
滑轮的轴是否随物体移动。要先确定滑轮轴的位置,分析它是与某个固定不动的物体连在一起,还是随物体一起移动,如果滑轮轴与固定不动的物体连在一起,不随物体移动,则为定滑轮
2.定滑轮和动滑轮的特点
【实验目的】探究定滑轮和动滑轮的特点。
【提出问题】(1)使用定滑轮动滑轮是否省力(或更费力)?
(2)使用定滑轮、动滑轮是否省距离(或需要移动更大的距离)?
(3)什么情况下使用定滑轮,什么情况下使用动滑轮?
【制订计划与设计实验】分别使同一物体在不使用滑轮、使用定滑轮、使用动滑轮时匀速运动,记录整个过程需要用力的大小、物体移动的距离及动力移动的距离、动力的方向,然后由数据分析得出结论。
【实验器材】钩码两个,滑轮两个,弹簧测力计一个等。
【实验过程】(1)按图12-2-4甲所示,
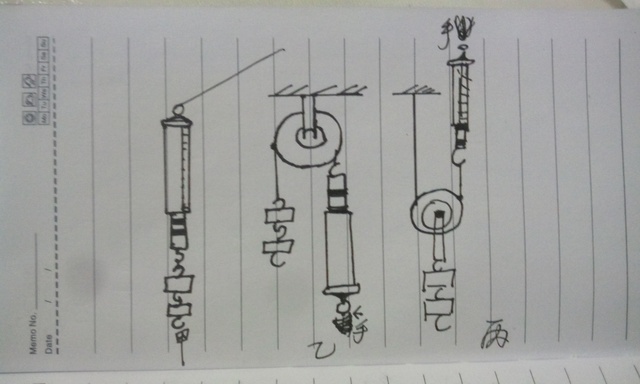
让钩码匀速上升的高度h=10cm,记录弹簧测力计的示数F,拉力方向及绳子自由端移动的距离s。
注意
用弹簧测力计直接拉钩码匀速上升,目的是使用滑轮时相比较。
(2)按图乙所示安装定滑轮,让钩码匀速上升的高度h=10cm,记录弹簧测力计的示数F、拉力方向及绳子自由端移动的距离s。
注意
(1)要匀速拉动弹簧测力计。
(2)定滑轮轴上可加润滑油,以减小摩擦力对实验的影响。
(3)选用质量较大的钩码。
(3)按图丙所示安装动滑轮,让钩码匀速上升的高度h=10cm,记录弹簧测力计的示数F、拉力方向及绳子自由端移动的距离s
注意
拉力要沿竖直向上的方向拉动物体和滑轮一起匀速缓慢上升。
(4)换用不同数量的钩码,重复上面的步骤。
注意
使用不同数量的钩码,以获得多组数据,使结论更具有普遍性。
【实验记录】滤,算了写吧

【交流论证】(1)对比用甲、乙两图所做实验记录的数据可知:使用定滑轮时,拉力F与钩码重力G相等,绳子自由端移动的距离s与钩码升高的高度h相同。(忽略绳子与滑轮间的摩擦力和滑轮与轴间的摩擦力、绳子的重力)
(2)对比用甲、丙两图所做实验记录的数据可知:使用动滑轮时,拉多G,绳子自由端移动的距离s=2h。(忽略动滑轮与绳的重力和摩擦力)
【实验结论】(1)使用定滑轮不省力,也不省距离,但可以改变力的方向。
(2)使用动滑轮可以省力,但不改变力的方向,而且费距离。
注意
(1)实验中应选用轻质的动滑轮。
(2)要始终竖直匀速拉动弹簧测力计。
(3)读数时,视线要与刻度盘垂直,不能静止读数。
(4)选择质量较小的动滑轮以减小动滑轮重力对实验的影响。
3.定滑轮和动滑轮的实质
(1)定滑轮可以看成一个变形的杠杆,如图12-2-5所示

,滑轮的轴相当于支点,动力臂和阻力臂都等于滑轮的半径,即l1=l2,根据杠杆的平衡条件Fl1=Gl2可知:F=G,即使用定滑轮不省力。可见,定滑轮的实质是一个等臂杠杆。
由于等臂杠杆不省力也不省距离,所以使用定滑轮时,物体上升的高度h和绳子自由端下降的距离s相等,
(2)动滑轮也可以看成一个变形的杠杆,
使用动滑轮能省一半力,则需费一倍的距离,即被提升的物体上升h,绳的自由端移动的距离s=2h,
4.使用定滑轮和动滑轮的几种情况(图中物体全部匀速运动,物体的重力都为G)

拓展
用平衡力知识研究定滑轮和动滑轮特点
如图12-2-9所示,对于定滑轮,在忽略摩擦时,物体受到拉力F和重力G作用,由于物体匀速上升则拉力F与重力G是一对平衡力,则F=G;对于动滑轮,在忽略摩擦和滑轮自重时,物体受到两段绳子的两个拉力F和重力G的作用,由于物体匀速上升,则2F=G,F=
1
2
G。
拓展
(1)使用定滑轮时,拉力F不沿竖直方向而改为其他方向时的拉力大小的分析:如图12-2-11所示

改变拉力F的方向,由图中的示意图可以得出l1=l2=r,由杠杆平衡条件知,F1=F2=G,(若考虑摩擦,则F>G)因此对于定滑轮来说,施加在绳端的力无论朝哪个方向,定滑轮都是一个等臂杠杆,在绳重和摩擦可以忽略不计的情况下,所用的拉力都等于物体的重力。
(2)对于动滑轮来说:①动滑轮在移动的过程中,支点也在不停地移动。②动滑轮省一半力的条件是:A.动滑轮与重物一起匀速移动; B.动力F的方向与物体移动的方向致;C.不计动滑轮重、绳重和摩擦。
知识点二 滑轮组
1.滑轮组在实际应用中,人们常常把定滑轮和动滑轮组合在一起,构成滑轮组。使用滑轮组既省力又可改变力的方向,但同时要多移动距离。
注意
滑轮组中的定滑轮起改变方向的作用;动滑轮起省力的作用。
2.与滑轮组有关的规律
(1)省力情况:忽略动滑轮的自重、绳重及摩擦,则拉力F=
1
n
G物,若考虑动滑轮自重G动,仅忽略绳重与摩擦,则F=
1
n
(G物+G动)(n为承担物重的绳子段数)。
滑轮组横放时,动滑轮上有几段绳子拉着物体做匀速直线运动,拉力的大小就是物体所受摩擦力的几分之一。不计绳与滑轮之间的摩擦时,F=
1
n
f物,此时绳子自由端移动的距离s与物体移动的距离s物的关系为s=ns物。
(2)移动距离:若物体升高h,绳子自由端移动的距离s=nh。
(3)移动速度:绳子自由端移动的速度v和物体移动速度v物之间的关系为v=nv物。
3.确定承担物重的绳子的段数n的方法
采用“分离法”:在定滑轮与动滑轮之间画一条虚线,只考虑与动滑轮相连的绳子段数,
4.滑轮组的组装
巧记
滑轮组组装口诀
“奇动偶定,一动配一定,偶数减一定,变向加一定。”
说明:(1)绳子段数为奇数时,绳子起点在动滑轮上;绳子段数为偶数时,绳子起点在定滑轮上。
(2)在不改变施力的方向时,以动滑轮个数为基数,按“一动配定,偶数减一定”来确定定滑轮的个数。即:一个动滑轮配一个定滑轮;但当n为偶数时,定滑轮的个数等于“动滑轮的个数减一个”。
(3)在需要改变施力的方向时,仍以动滑轮的个数为基数,按“变向加一定”的方法确定定滑轮的个数。
即:在“一动配一定,偶数减一定”的基数上,若变向再加上一个定滑轮。
知识点三 轮轴和斜面
1.轮轴
(1)轮轴:轮轴由具有共同转动轴的大轮和小轮组成,通常把大轮叫轮,小轮叫轴。辘轳、方向盘、水龙头等都属于轮轴。
(2)轮轴的实质:轮轴可看成杠杆的变形,
(3)轮轴的特点:当把动力施加在轮上,阻力施加在轴上时,则动力臂l1=R,阻力臂l2=r,根据杠杆的平衡条件F1l1=F2l2,得F1R=F2r,可见轮半径是轴半径的几倍,动力就是阻力的几分之一,因此使用轮轴可以省力,但要费距离。
注意
当把动力施加在轴上时,此时由于轴半径小于轮半径,如图12-2-23所示

,根据杠杆的平衡条件F1l1=F2l2,得F1r=F2R,由于R>r,则F1>F2,即使用轮轴费力,但节省距离。因此不要错误地认为使用轮轴一定省力,关键是看动力施加在轮上还是轴上。
2.斜面
(1)倾斜的木板、弯曲的盘山公路都构成了斜面。
斜面是一种可以省力的简单机械,却费距离。
(2)如图12-2-25所示

,当斜面高度h一定时,斜面l越长,越省力(即F越小);当斜面长l相同时,斜面高h越小,越省力(即F越小);当斜面l越长,斜面高h越小时,越省力(即F越小)。理想情况下斜面公式:Fl=Gh。
斜面长(l)是斜面高(h)的几倍,所用的拉力F就是物重G的几分之一。
3.各种简单机械的对比
拓展
盘山公路修得“曲曲折折”,目的是通过增加斜面的长,即多移动距离,达到省力的目的。
有的同学骑自行车上坡时喜欢走“S”形,更容易上坡,这便是利用了多移动距离达到省力的效果,所以更容易爬上坡去。
易误点 不会分析结构特殊的滑轮组。
【易误点辨析】如图12-2-40所示的滑轮组结构较为特殊,分析思路如下:
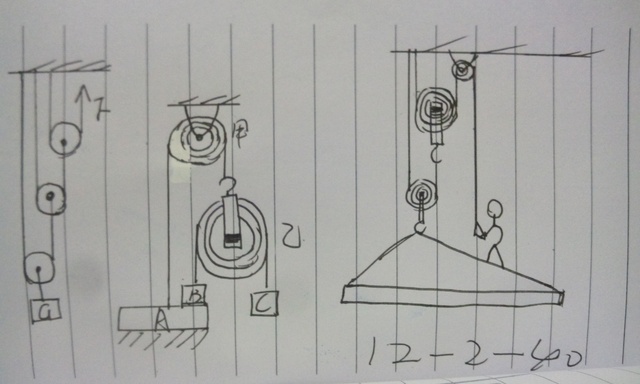
(1)在不计绳重和摩擦时,同一根绳子两端的拉力相等;
(2)对滑轮组受力分析时,灵活运用整体法或隔离法;
(3)对于结构比较特殊的滑轮组,选择合适的切入点进行受力分析。